最近开始入门脉冲神经网络,本来想用这个做个单神经元XOR,结果发现1993年的同行们已经发过论文了,而且还设计了4种不同的神经元。我想把论文下载来看看,结果因为没用校园网,被施普林格拦住了,想在家下载还得花美元。下个论文跟遇见个拦路抢劫的似的,这上哪说理去。没辙,等开学回学校再说吧。
同行们做过了,门还是得入。这次用Java实现了Hodgkin-Huxley模型的模拟,与论文中的图形大体一致。
Hodgkin-Huxley模型的原始论文「A QUANTITATIVE DESCRIPTION OF MEMBRANE CURRENT AND ITS APPLICATION TO CONDUCTION AND EXCITATION IN NERVE」中给出了膜电位对时间的变化(微分方程)。对于一个给定电流,求膜电位的方法有二:其一是代入方程组后利用MATLAB等工具求出膜电位关于时间的解析解,但某些情况下可能解不出来。其二是利用欧拉方法一点点累计计算出数值解。前者没有误差但求解微分方程的过程较为费劲,后者实现起来比较方便,但是对于较大时间范围的模拟时会累积误差。
按照原论文518页(页面上面的页码)下方和519页上方的公式,及520页Table 3中的实验数据实现了如下程序。刺激电流恒定为50毫安。
理论上可以用MATLAB求出给定电流下的膜电位表达式,但是我MATLAB不熟,没整出来,直接上Java代码吧。
import java.io.File
import java.io.PrintWriter
import java.nio.charset.StandardCharsets
import kotlin.math.exp
import kotlin.math.pow
class HodgkinHuxleyModel(private val duration: Double, private val deltaT: Double = 0.01) {
//From Table 3
private val membraneCapacitance = 1.0 //uF
private val reversalPotentialNa = 115.0 //mV
private val reversalPotentialK = -12.0 //mV
private val reversalPotentialLeak = 10.613 //mV
private val averageConductanceOfNa = 120.0 //mΩ-1
private val averageConductanceOfK = 36.0 //mΩ-1
private val averageConductanceOfLeak = 0.3 //mΩ-1
//Cell status: <time, value>
val voltage = HashMap<Double, Double>()
val gateN = HashMap<Double, Double>()
val gateM = HashMap<Double, Double>()
val gateH = HashMap<Double, Double>()
val currentOfNa = HashMap<Double, Double>()
val currentOfK = HashMap<Double, Double>()
val currentOfLeak = HashMap<Double, Double>()
val currentOfCapacitance = HashMap<Double, Double>()
private var currentTime: Double = 0.0
//formula from paper
private fun alphaN(): Double = 0.01 * (10.0 - voltage[currentTime]!!) / (exp((10.0 - voltage[currentTime]!!) / 10.0) - 1)
private fun betaN(): Double = 0.125 * exp(-voltage[currentTime]!! / 80.0)
private fun alphaM(): Double = 0.1 * (25.0 - voltage[currentTime]!!) / (exp((25.0 - voltage[currentTime]!!) / 10.0) - 1)
private fun betaM(): Double = 4.0 * exp(-voltage[currentTime]!! / 18.0)
private fun alphaH(): Double = 0.07 * exp(-voltage[currentTime]!! / 20.0)
private fun betaH(): Double = 1.0 / (exp((30.0 - voltage[currentTime]!!) / 10.0) + 1)
//Set initial status
init {
voltage[currentTime] = 0.0
gateN[currentTime] = alphaN() / (alphaN() + betaN())
gateM[currentTime] = alphaM() / (alphaM() + betaM())
gateH[currentTime] = alphaH() / (alphaH() + betaH())
}
//given I(currentTime) calculate status at currentTime+deltaT
private fun iterate(current: Double) {
currentOfNa[currentTime] =
averageConductanceOfNa * gateM[currentTime]!!.pow(3) * gateH[currentTime]!! * (voltage[currentTime]!! - reversalPotentialNa)
currentOfK[currentTime] =
averageConductanceOfK * gateN[currentTime]!!.pow(4) * (voltage[currentTime]!! - reversalPotentialK)
currentOfLeak[currentTime] = averageConductanceOfLeak * (voltage[currentTime]!! - reversalPotentialLeak)
currentOfCapacitance[currentTime] =
current - currentOfNa[currentTime]!! - currentOfK[currentTime]!! - currentOfLeak[currentTime]!!
voltage[currentTime + deltaT] =
voltage[currentTime]!! + deltaT * currentOfCapacitance[currentTime]!! / membraneCapacitance
gateN[currentTime + deltaT] =
gateN[currentTime]!! + deltaT * (alphaN() * (1 - gateN[currentTime]!!) - betaN() * gateN[currentTime]!!)
gateM[currentTime + deltaT] =
gateM[currentTime]!! + deltaT * (alphaM() * (1 - gateM[currentTime]!!) - betaM() * gateM[currentTime]!!)
gateH[currentTime + deltaT] =
gateH[currentTime]!! + deltaT * (alphaH() * (1 - gateH[currentTime]!!) - betaH() * gateH[currentTime]!!)
currentTime += deltaT
}
//Given I(t) do whole procedure
fun run(current: (Double) -> (Double)) {
while (currentTime <= duration)
iterate(current(currentTime))
}
//save to csv file, time for ms
fun writeToCsv(filename: String) {
val writer = PrintWriter(File(filename), StandardCharsets.UTF_8)
writer.println("time,n,m,h,Na+ current,K+ current,leak current,capacitance current,membrane potential")
voltage.keys.sorted().forEach { k ->
writer.println("$k,${gateN[k]},${gateM[k]},${gateH[k]},${currentOfNa[k]},${currentOfK[k]},${currentOfLeak[k]},${currentOfCapacitance[k]},${voltage[k]}")
}
writer.close()
}
}这个是模拟细胞的类,主函数如下(复现原论文525页的图形)。
import com.panayotis.gnuplot.JavaPlot
fun main() {
//convert HashMap to GnuPlot points set
fun HashMap<Double, Double>.toCurveArray(): Array<DoubleArray>{
val result = ArrayList<DoubleArray>()
this.forEach {
result.add(doubleArrayOf(it.key, it.value))
}
return result.toTypedArray()
}
//simulate 0 to 6ms, step 0.01ms
val neuron = HodgkinHuxleyModel(6.0, 0.01)
//I(t) = 50mA
neuron.run { 50.0 }
//plot voltage data
val p = JavaPlot()
p.addPlot(neural.voltage.toCurveArray())
p.plot()
}其中依赖JavaPlot调用GnuPlot将电压对时间的数据绘制出来,运行结果如下:
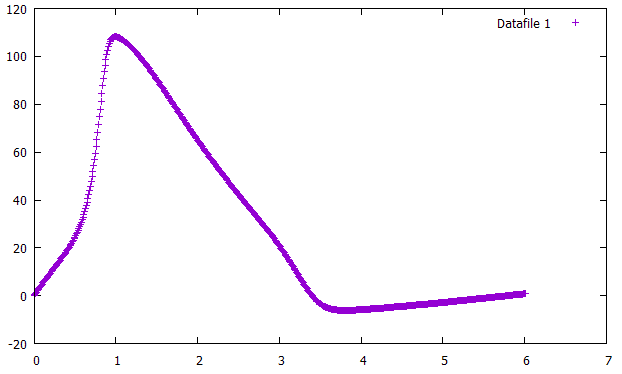
通过在调用neuron.run时传入不同的电流可以得到不同的效果。同时还可以改变神经元本身的各种参数来达成不同的特性。
-全文完-

【代码札记】Java实现欧拉方法模拟导纳恒定的Hodgkin-Huxley模型 由 天空 Blond 采用 知识共享 署名 - 非商业性使用 - 相同方式共享 4.0 国际 许可协议进行许可。
本许可协议授权之外的使用权限可以从 https://skyblond.info/about.html 处获得。