MENU

《医疗人工智能》课程报告

July 13, 2021 • 瞎折腾

想来上一次更新还是5月底。整个六月都在搞考试和比赛的事情。考试就是期末考试，计算机本科专业得益于贯通班（北京市高端技术技能人才贯通培养项目）的存在，出题老师不得不将试卷难度一降再降，最后活脱脱把计算机专业课考试搞成了语文默写，太傻逼了。竞赛则是之前参加的一个Neo N3区块链的黑客松，前天正式提交了项目，之后的事情就交给评委吧。

在此期间，学校的小学期也开始了。这次小学期听说来了个哈佛的终身助理教授终身助教来给讲课，我觉得讲的还行。于是就把这个课程的报告贴出来，补上六月的更新。

线性回归

基于大脑体积预测大脑重量

该实验使用线性回归模型，利用大脑体积对大脑重量进行预测。

输入特征

本模型只有一个输入特征：

  • 大脑体积：以立方厘米为单位

预测结果

image-20210708183520715.png

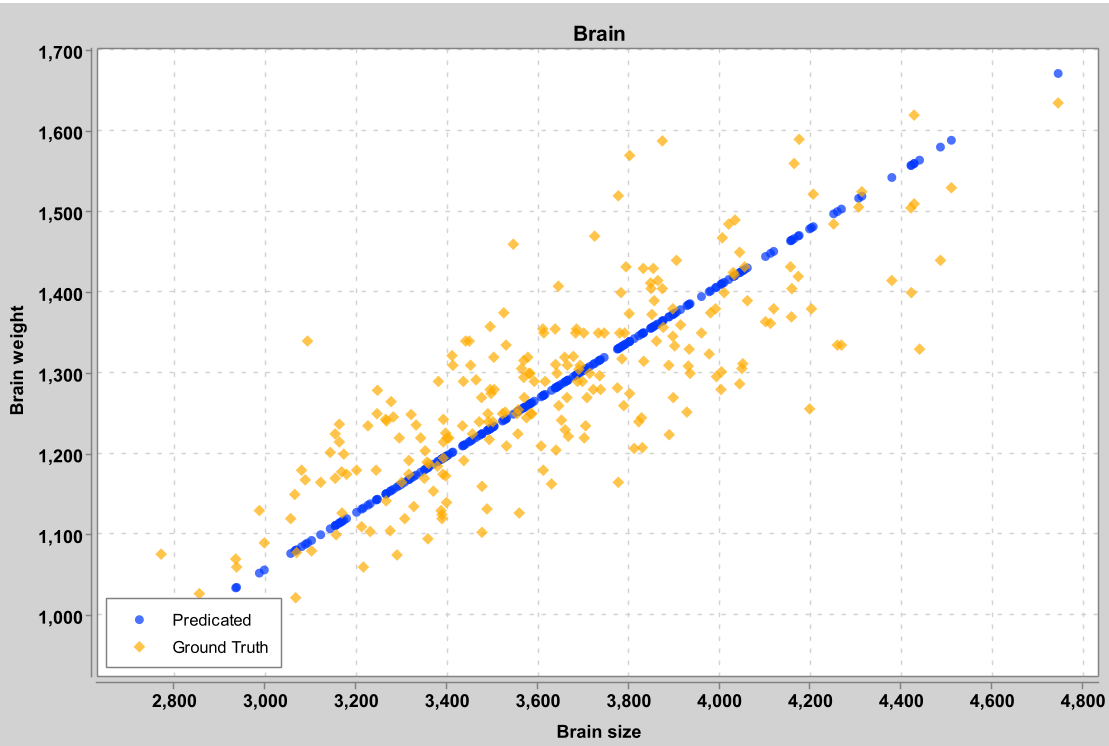
横坐标为输入，即大脑体积；纵坐标（输出）为大脑重量（以克为单位）。

橙色散点为真实值，蓝色的点为模型的预测。

房价预测

该实验使用线性回归模型，利用与住宅相关的多种数据对住宅价格进行预测。

输入特征

该模型具有多个输入特征：

  • CRIM：房子所在街区的犯罪率
  • ZN：划分为大于 25,000 平方英尺的住宅用地的比例。
  • INDUS：房子所在街区的非零售营业面积占比
  • CHAS：Charles River虚变量，为1表示tract bounds river
  • NOX：一氧化氮浓度（百万分之一）
  • RM：每个住宅的平均房间数
  • AGE：1940 年之前建造的自住单元的比例
  • DIS：到五个波士顿就业中心的加权距离
  • RAD：径向公路可达性指数
  • TAX：每 10,000 美元的全值财产税率
  • PTRATIO：按城镇划分的师生比例
  • B：1000(Bk — 0.63)²，其中 Bk 是按城镇划分的非裔美国人后裔的比例
  • LSTAT：人口较低地位的百分比

预测结果

image-20210708183804966.png

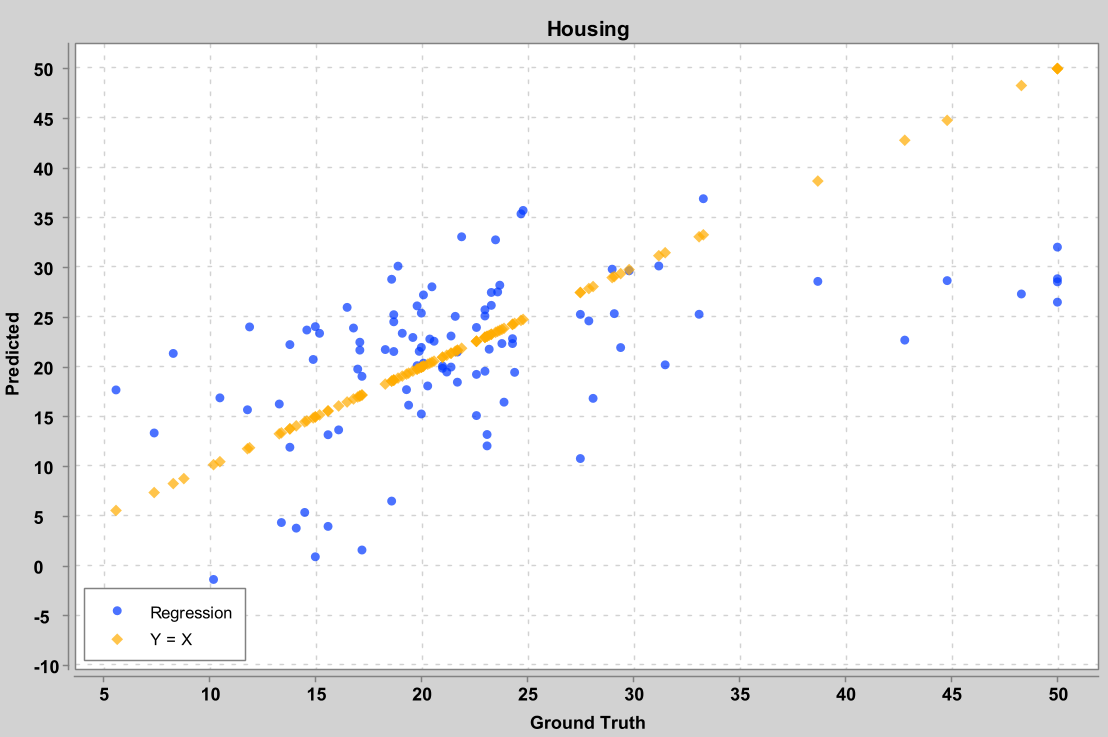
模型预测已有住户房屋的价值的中间值，以一千美元为单位衡量。

横坐标为真实值，纵坐标为预测值，其中橙色的点为Y=X，表示预测值等于真实值，作为衡量模型表现的参考。蓝色点为模型表现，对应每一个真实值与预测值元组。

模型解释

本次实验使用到了SameDiff库，该库是JVM平台上的自动微分库，其功能类似Tensorflow，能够通过给定的正向操作自动对损失变量求梯度。

$X$是特征输入，其形状为[BatchSize, InputSize]；$Y$是对应特征的输出，其形状为[BatchSize, OutputSize]。

模型的参数有两个：

  • $W$形状为[InputSize, OutputSize]
  • $B$形状为[OutputSize]

模型的预测值：

$$ Y' = X \cdot W + B $$

预测值与真实值的差距：

$$ D = Y' - Y $$

模型损失：

$$ L = mean(D^2) $$

其中$mean(\cdot)$表示求平均。

学习时利用对$L$的梯度更新参数$W$和$B$：

$$ W = W - \alpha \cdot gradW $$

$$ B = B - \alpha \cdot gradB $$

其中$gradW$和$gradB$表示由SameDiff自动计算的梯度，$\alpha$表示学习率。

逻辑回归

糖尿病预测

本实验使用逻辑回归模型，基于多项生理数据对糖尿病进行预测。

输入特征

本模型具有多个输入特征：

  • Pregnancies：孕期，以周为单位
  • Glucose：血糖水平，以mg/dL为单位
  • BloodPressure：血压，以mmHg为单位
  • SkinThickness：皮肤厚度，以毫米为单位
  • Insulin：胰岛素水平，以单位（unit）衡量
  • BMI：身高体重指数
  • DiabetesPedigreeFunction：糖尿病遗传系数
  • Age：年龄

血糖数据分类可视化

由于糖尿病最典型的生理特征是血糖变化，因此我对血糖数据进行了分类可视化：

image-20210708195622800.png

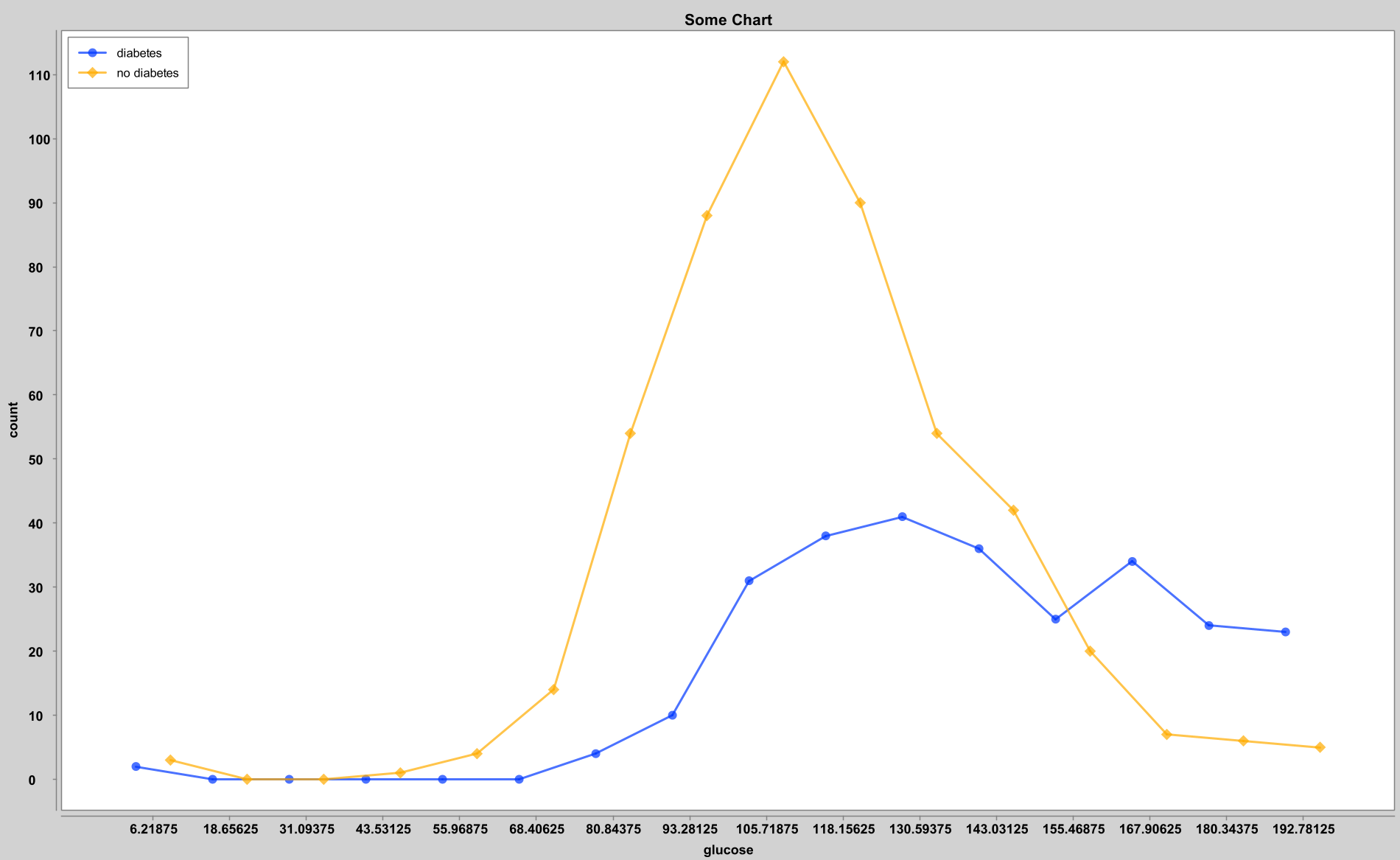
图中横坐标为血糖水平，纵坐标表示该血糖水平下的样本数量。黄色为未患病样本，可见其形状更接近于正态分布。而蓝色则是患病样本的数据，显然患糖尿病的样本更多分布在高血糖部分。

预测结果

模型在测试集上的混淆矩阵如下：

预测为不患病预测为患病
实际不患病8810
实际患病3323

模型的具体分数如下：

  • Accuracy：0.7208
  • Precision：0.6970
  • Recall：0.4107
  • F1：0.5169

模型解释

$X$是特征输入，其形状为[BatchSize, InputSize]；$Y$是对应特征的输出，其形状为[BatchSize, OutputSize]，其中$y_i$的值应该是0或1，而不应当出现其他值。

模型的参数有两个：

  • $W$形状为[InputSize, OutputSize]
  • $B$形状为[OutputSize]

模型的预测值：

$$ Y' = \sigma(X \cdot W + B) $$

其中:

$$ \sigma(X) = \frac{1}{1+e^{-X}} $$

模型损失（交叉熵）：

$$ L = -\frac{1}{BatchSize}\sum_{i=1}^{OutputSize} Y_i \cdot logY'_i + (1 - Y_i)log(1-Y'_i) $$

其中$Y_i$表示$Y$的第$i$个样本。

学习时利用对$L$的梯度更新参数$W$和$B$：

$$ W = W - \alpha \cdot gradW $$

$$ B = B - \alpha \cdot gradB $$

其中$gradW$和$gradB$表示对$L$自动计算的梯度，$\alpha$表示学习率。

神经网络

心脏病预测

该模型通过多个生理指标对是否患有心脏病进行预测：

输入特征

该模型具有多个输入特征：

  • age：年龄

  • sex：性别

    • 0：女性
    • 1：男性

  • cp：胸痛分类

    • 1：典型心绞痛
    • 2：非典型心绞痛
    • 3：非心绞痛
    • 4：无症状
  • trestbps：舒张压，以mmHg为单位
  • chol：血清胆固醇水平，以mg/dL为单位

  • fbs：空腹血糖

    • 1：空腹血糖高于120mg/dL
    • 0：空腹血糖低于或等于120mg/dL

  • restecg：静息状态心电图结果：

    • 0：正常
    • 1：ST-T波异常（T波倒置和/或ST段偏差大于0.05毫伏）
    • 2：根据Estes标准表明可能或明确的左心室肥厚
  • thalach：最大心率

  • exang：运动诱发心绞痛

    • 1：有
    • 0：无

  • oldpeak：运动引起的ST电压降低

    • 1：有
    • 0：无

  • slope：峰值运动ST段斜率

    • 1：升高
    • 2：平坦
    • 3：下降
  • ca：荧光检查着色的主要血管数（0~3）

  • thal：地中海贫血

    • 3：正常
    • 6：固定缺陷
    • 7：可逆缺陷

预测结果

Loss与迭代关系图：

image-20210708203037104.png

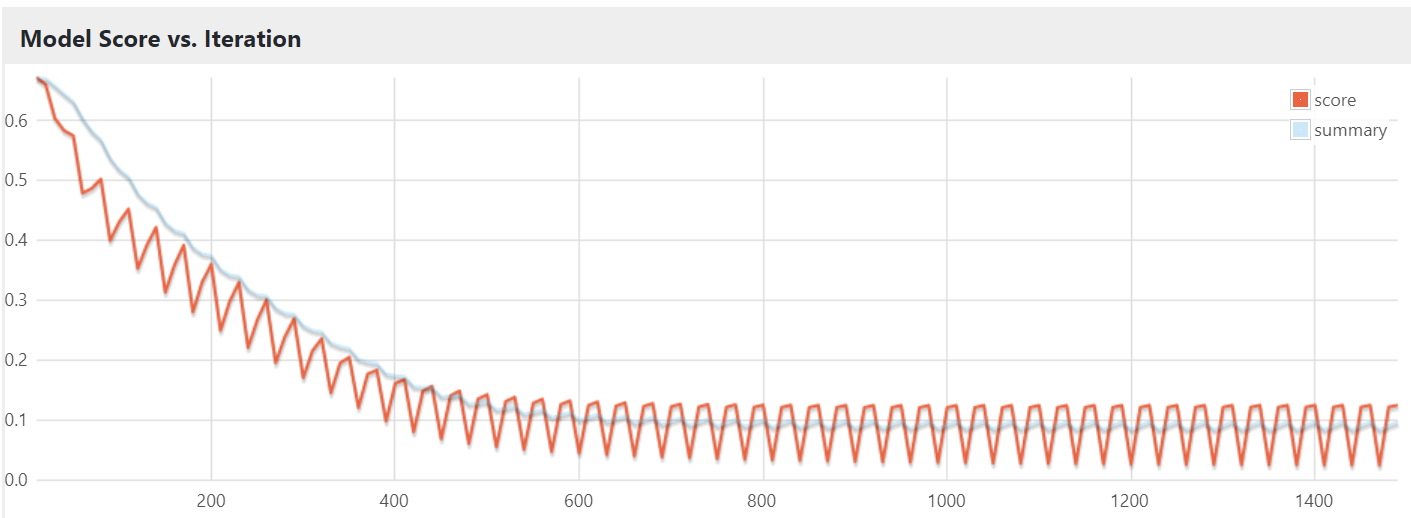
在测试集上的混淆矩阵：

预测为不患病预测为患病
实际不患病217
实际患病627

模型分数：

  • Accuracy：0.7869
  • Precision：0.7941
  • Recall：0.8182
  • F1 Score：0.8060

模型解释

本模型使用多层感知机网络，本质上即多个逻辑回归的堆叠。

多层感知机网络结构如下：

1_Pn42wNB6_HBKgpvxRzGBWw.png

第$i$层隐藏层的输出：

$$ Y_i' = \sigma(Y_{i-1}'\cdot W_i + B_i) $$

其中$Y_i'$是第$i$层的输出值，$Y_{i-1}'$是第$i-1$层的输出值，$W_i$是第$i$层的权重矩阵，$B_i$是第$i$层的偏置值矩阵，$\sigma(\cdot)$是激活函数。

损失函数使用交叉熵损失函数，即公式$(8)$。

梯度更新不变，但需要使用反向传播，即计算网络输出时从输入层向输出层计算（$i$递增），而计算和更新梯度时，从输出层入手计算出网络的损失，然后依次求出本层梯度，并将梯度传到上一层（$i$递减）。其中非输出层的梯度需要经过链式求导法则间接求出。

卷积神经网络

新冠肺炎CT成像预测

本模型以肺部CT图片为输入，预测就诊者是否感染一般肺炎或新冠肺炎。

输入特征

本模型以肺部CT图片为输入。图片将被转换成单通道灰度图片，并压缩到192x192大小。

健康样本的肺部CT：

image-20210708204527492.png

新冠肺炎样本的肺部CT：

image-20210708204500128.png

其他病毒导致肺炎的肺部CT：

image-20210708204609951.png

预测结果

image-20210708204700746.png

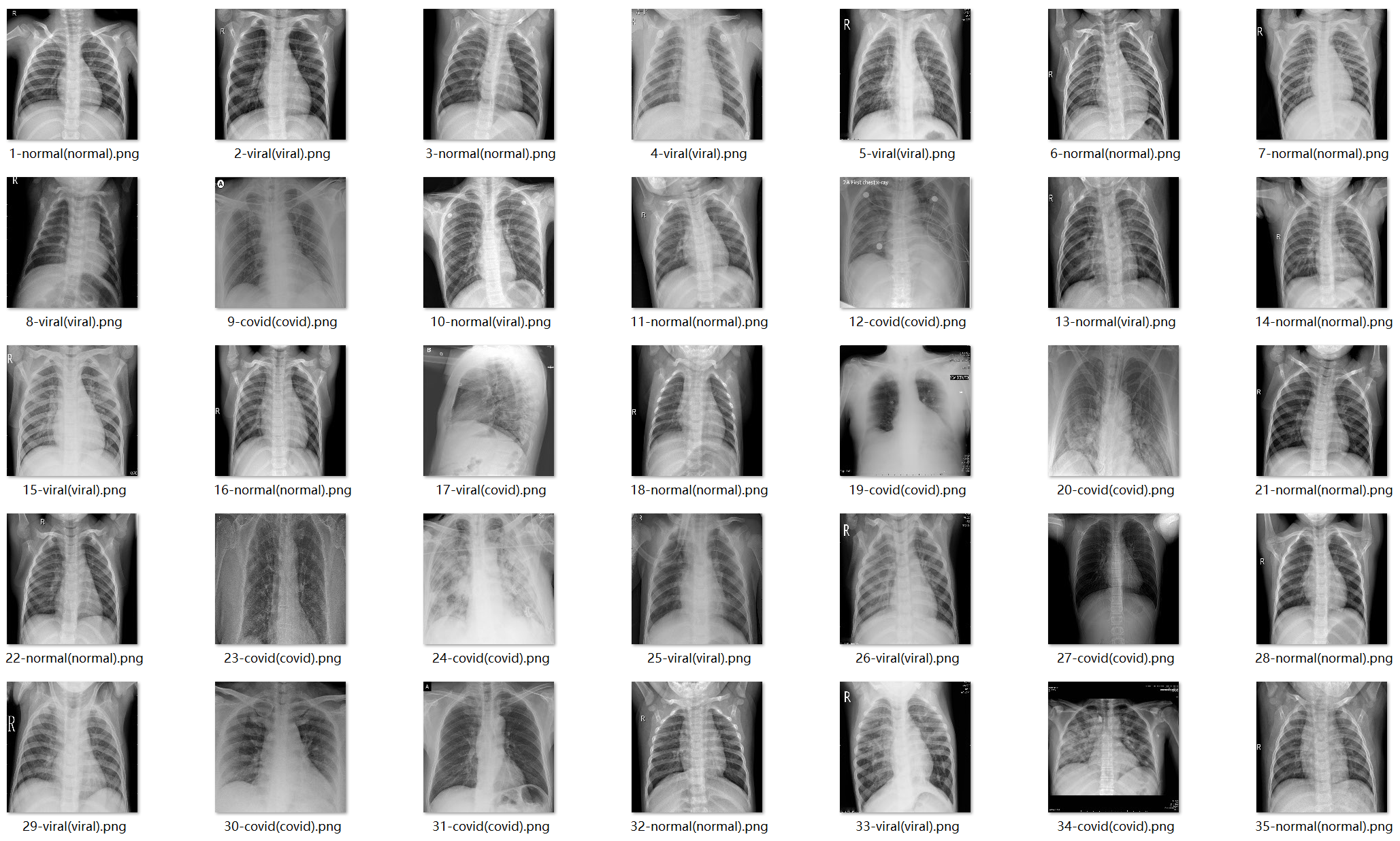
每张测试图片命名格式为【序号】-【预测值】(【真实值】).png。

程序根据模型给出的三种结果的概率，取最大的一个概率作为预测结果。一共有三种可能：

  • covid：患有新冠肺炎
  • normal：健康
  • viral：其他病毒引起的肺炎

在测试集上的混淆矩阵为：

预测为新冠预测为健康预测为病毒
实际为新冠2514
实际为健康0300
实际为病毒1227

模型分数：

  • Accuracy：0.9111
  • Precision：0.9139
  • Recall：0.9111
  • F1 Score：0.9102

模型解释

本模型使用经典的LeNet结构，选用ReLU作为全连接层的激活函数。

LeNet结构如下：

0_-1Pad7loK_dFOUvS.png

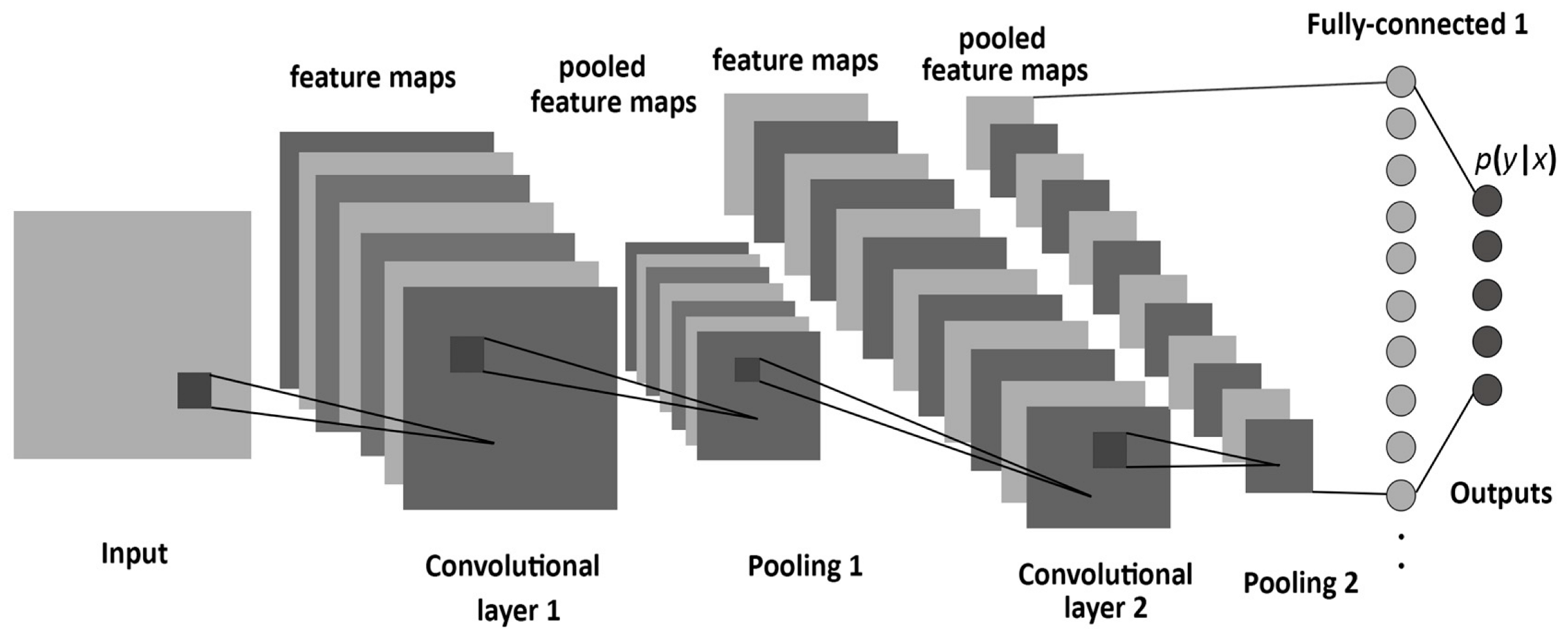
LeNet的主要特征是以一层卷积和一层池化为一组，连续两组，随后转全连接层进行多分类。

其中卷积层的作用为提取特征，通过滑动卷积核，将卷积核与输入矩阵重叠的部分对位相乘并求和，作为当前层该卷积核通道的输出。每层可具有多个卷积核，每个卷积核输出一个通道，因此输入输出的形状为[BatchSize, ChannelSize, Height, Width]。

池化层用以进一步压缩输入尺寸。按照给定的大小将输入划分为多个区域，每个区域根据池化方法不同，计算该区域的最大值或平均值，以该值代替整个区域。池化层不改变通道数量，只改变每个通道的宽度和高度。

最后一个池化层的输出将被展开成低维度的向量，输入全连接层，即前述的多层感知机网络，该网络使用ReLU作为激活函数。

ReLU：

$$ ReLU(x) = max(0, x) $$

输出层使用SoftMax作为激活函数。SoftMax：

$$ \sigma(\mathbf{z})_i = \frac{e^{z_i}}{\sum_{i=1}^{OutputSize} e^{z_i}} $$

其中$i$从$1$遍历到$OutputSize$。该激活函数保证所有分类的输出值和一定为1。

输出层的损失函数为负对数似然损失函数：

$$ L = - logY_i $$

循环神经网络

新冠肺炎确诊人数趋势预测

本实验使用长短期记忆网络，利用前一天的新冠肺炎确诊人数预测第二天的确诊人数。

输入特征

该模型仅有一个输入特征：

  • 前一天的统计人数（2020年1月22日~同年7月11日）

预测结果

image-20210708211819930.png

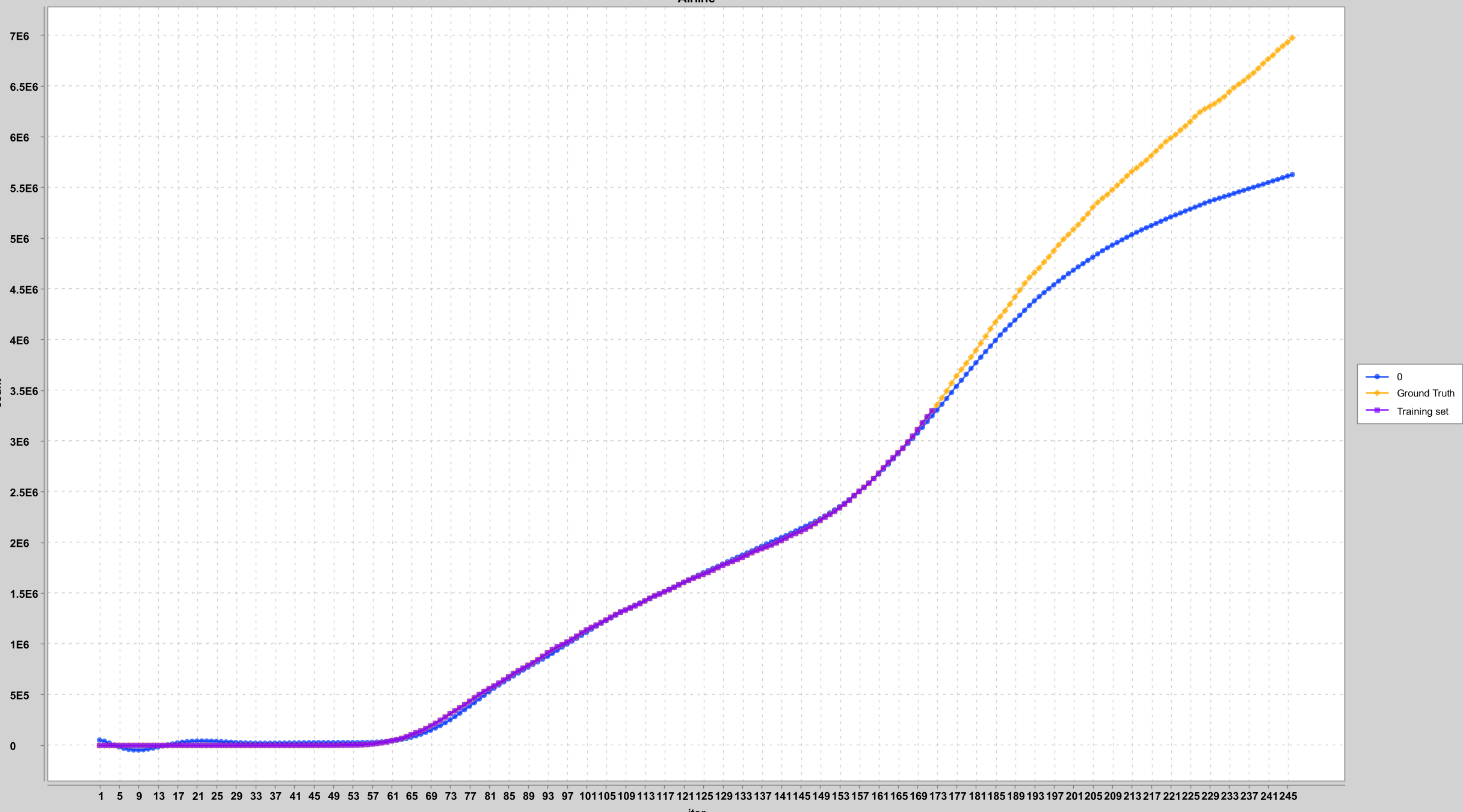
横轴为天数（第一天为T=1），纵轴为人数。其中黄色线为真实值，紫色线为用于训练的数据，蓝色线为模型的预测值。

模型解释

循环神经网络为时序敏感的网络。在任意$t$时刻：输入为$x^{(t)}$，

神经元的隐藏状态：

$$ h^{(t)} = \sigma_1(Ux^{(t)} + Wh^{(t-1)} + b) $$

神经元的输出：

$$ y'^{(t)} = \sigma_2(o^{(t)}) = \sigma_2(Vh^{(t)} + c) $$

可以看出，除了每一时刻的输入外，神经元内部还有一个隐藏状态，充当该神经元对于过去输入的记忆。

而长短期记忆网络（LSTM）则引入门控机制，使得这类神经元能够同时保持长期和短期记忆。

1_0R9LrwwY4zd585qEAgws6w.png

LSTM神经元除了上面的$h^{(t)}$外，每时刻还存在一个细胞状态矩阵$C^{(t)}$，同时还有遗忘门、输入门和输出门。

遗忘门：

$$ f^{(t)} = \sigma(W_fh^{(t-1)} + U_fx^{(t)} + b_f) $$

该值代表了根据当前输入，细胞遗忘上一层细胞状态的概率。

输入门：

$$ i^{(t)} = \sigma(W_ih^{(t-1)} + U_ix^{(t)} + b_i) $$

$$ a^{(t)} = tanh(W_ah^{(t-1)} + U_ax^{(t)} + b_a) $$

其中$i^{(t)}$决定当前输入被细胞状态记住的概率矩阵，$a^{(t)}$是被记住的数据。

细胞状态更新：

$$ C^{(t)} = C^{(t-1)}\odot f^{(t)} + i^{(t)} \odot a^{(t)} $$

其中$\odot$为基本积，即每个元素对位相乘。

输出门：

$$ o^{(t)} = \sigma(W_oh^{(t-1)} + U_ox^{(t)} + b_o) $$

$$ h^{(t)} = o^{(t)}\odot tanh(C^{(t)}) $$

原理与输入门更新细胞状态类似。$h^{(t)}$将作为神经元在$t$时刻的输出。

深度学习网络模型部署

本实验将前面实验中的神经网络封装成应用，打包，部署到云端，成为一个云服务。

系统背景介绍

该系统选取之前的卷积神经网络实验，将对肺部CT进行肺炎预测的模型封装成网页应用，模拟在医院情境中，患者使用该系统自主判断病情，由医生进行最终判断的需求用例。该系统意图减轻医生的压力：由神经网络进行判断，由医生对结果进行复审。

系统前端输入

该系统的前端设计简洁而明确。由于该模型的输入只有一张CT图片，因此前端直接提示用户上传一张医学影像图片。

image-20210708223438399.png

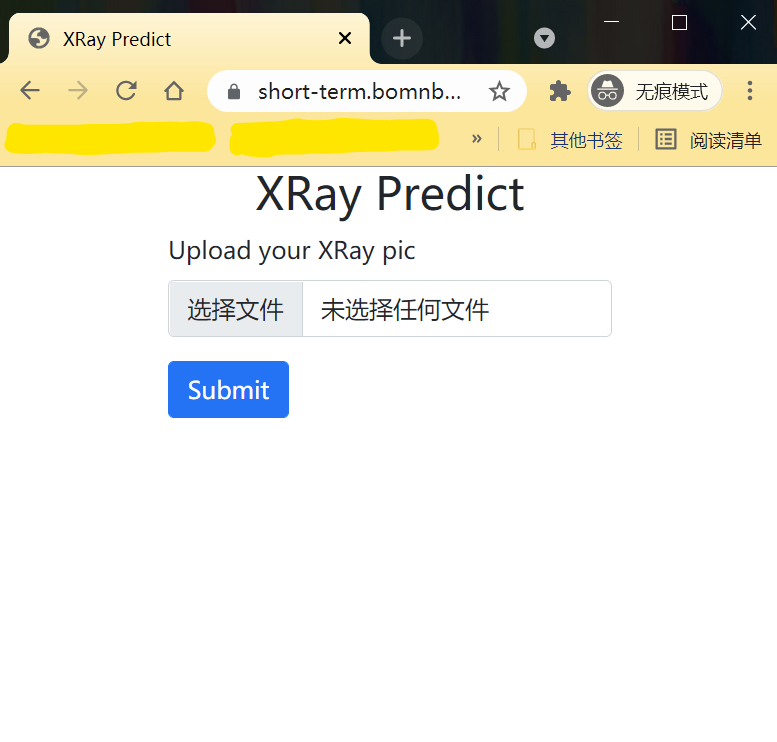
用户选择图片并提交后将跳转到结果页面，该页面将包含模型预测的结果。

系统结果输出

image-20210708223754668.png

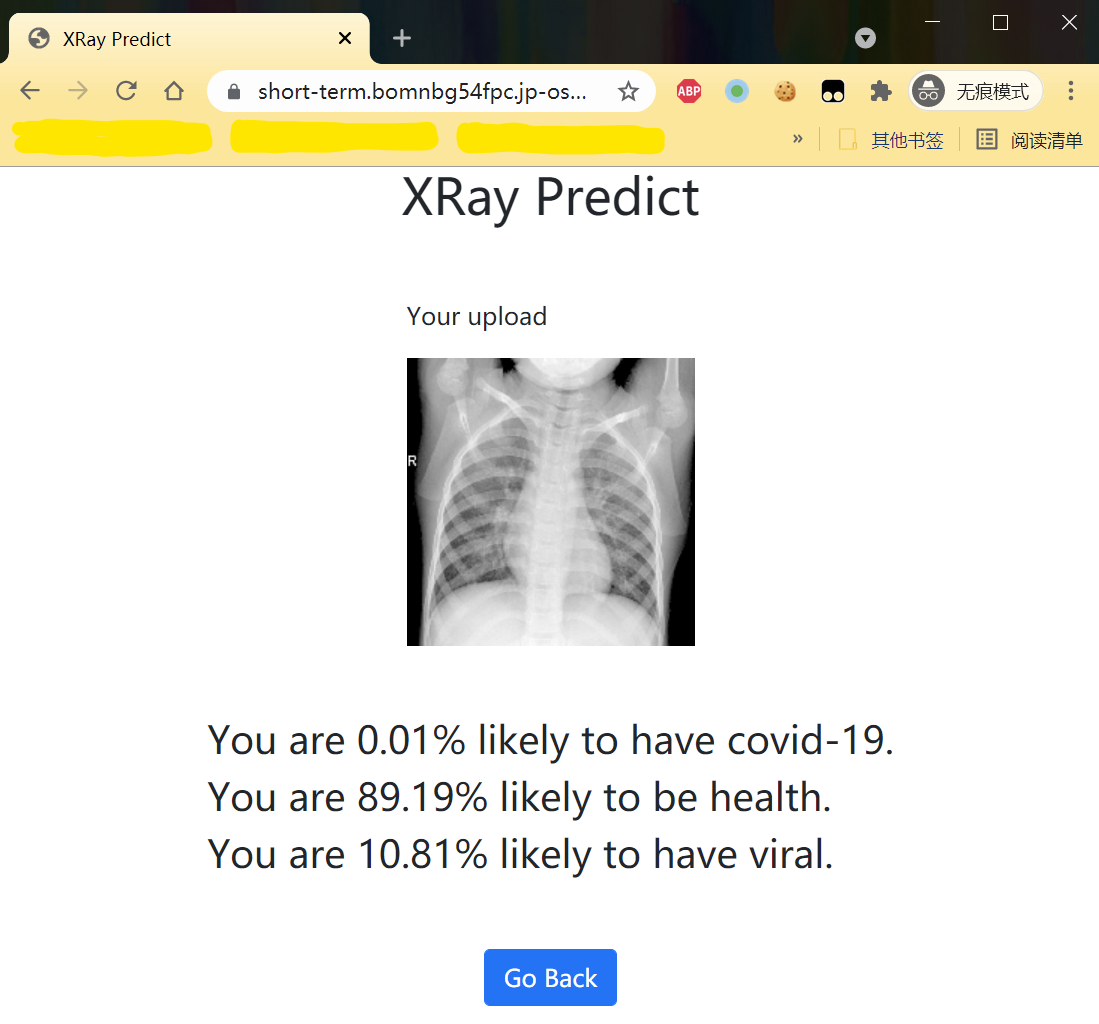
结果页面将附上用户上传的图片，并给出如下三种情况的概率：

  • 患有新冠肺炎
  • 没有感染任何肺炎（健康）
  • 患有病毒引起的肺炎

系统部署上云

本系统基于JVM构建，因此可以跨平台部署到云端环境。这里我选用IBM Cloud提供的Code Engine服务。该服务通过预先构建的Docker镜像部署应用程序，并自动生成API接口。同时该平台提供可供缩放的执行环境，可以实现高性能计算，同时在没有访问请求的情况下自动缩减资源，以便减小成本，而在访问量增加时自动扩展并部署程序，以便及时响应增加的请求。

基于该程序构建的Docker镜像包含必要的网页模板、Java应用程序和实现训练好的模型。具体镜像可以在Docker Hub上找到：https://hub.docker.com/r/hurui200320/short-term

关于IBM Code Engine的配置不再赘述，由于模型本身大小为544MB，加上JVM运行时所需的内存，我在配置中选择了4核心8GB内存的配置，并设置最小实例数量为0，即没有请求的时候完全关闭所有部署实例，以节省成本。实例将在第一个请求到达后立刻开始部署，完成后将响应用户的请求。

后记

本课程使用Java实现，代码上并没有什么奇巧淫记，都是按照深度学习库的文档写的，所以就不放代码了。

相关依赖如下：

// Basic env
implementation "org.jetbrains.kotlin:kotlin-stdlib-jdk8:1.5.20"
implementation "ch.qos.logback:logback-classic:1.2.3"

// Utils
implementation group: 'com.opencsv', name: 'opencsv', version: '5.5'
implementation 'org.knowm.xchart:xchart:3.8.0'

// Javalin and template
implementation 'io.javalin:javalin:3.13.9'
implementation 'gg.jte:jte:1.10.0'

// Deeplearning4j
implementation 'org.deeplearning4j:deeplearning4j-core:1.0.0-beta7'
implementation 'org.deeplearning4j:deeplearning4j-ui:1.0.0-beta7'
implementation 'org.nd4j:nd4j-native:1.0.0-beta7'
implementation 'org.nd4j:nd4j-native:1.0.0-beta7:windows-x86_64-avx2'

知识共享许可协议
《医疗人工智能》课程报告 由 天空 Blond 采用 知识共享 署名 - 非商业性使用 - 相同方式共享 4.0 国际 许可协议进行许可。
本许可协议授权之外的使用权限可以从 https://skyblond.info/about.html 处获得。

报告人工智能神经网络医疗人工智能
Archives QR Code
QR Code for this page
Tipping QR Code
Leave a Comment