【歪门邪道】在 Logisim 中实现32位超前进位加法器

这学期的课程普遍偏向硬件部分，正好我也补一补在硬件知识上的短缺。众所不一定周知，我这几年一直是在JVM上摸爬滚打，在硬件方面的发展早在六七年前就停了，一方面是家里不太适合放那些零碎的芯片，另一方面买芯片确实是得花钱，而写程序恰好还就能省钱。所以迫于金钱所困，十二岁从硬件入门这方面，两三年之后便开始转向Java的阵营（还是得说，Java天下第一，不接受其他任何观点），直至最近。上学期学了门数字逻辑，一下子觉得FPGA挺有意思，寒假也买了块学校同款芯片的FPGA开发板，是真他娘的贵，但是确实是有意思。遂决定趁此学期好好巩固一下硬件。（题外话：课余学习日语的计划真是荒废了好几年了，看来今年也够呛了呢）

本文将记述我在Logisim中搭建一个32位加法器的过程。

题外话

今天上完计算机组成原理，遂开始写作业，发现有这么一道题：

设机器字长为32位，用与非门和与或非门设计一个并行加法器（假设与非门的延迟时间为30ns，与或非门的延迟时间为45ns），要求完成32位加法时间不得超过0.6μs。画出进位链及加法器逻辑框图。

我的作业画风是这样的：

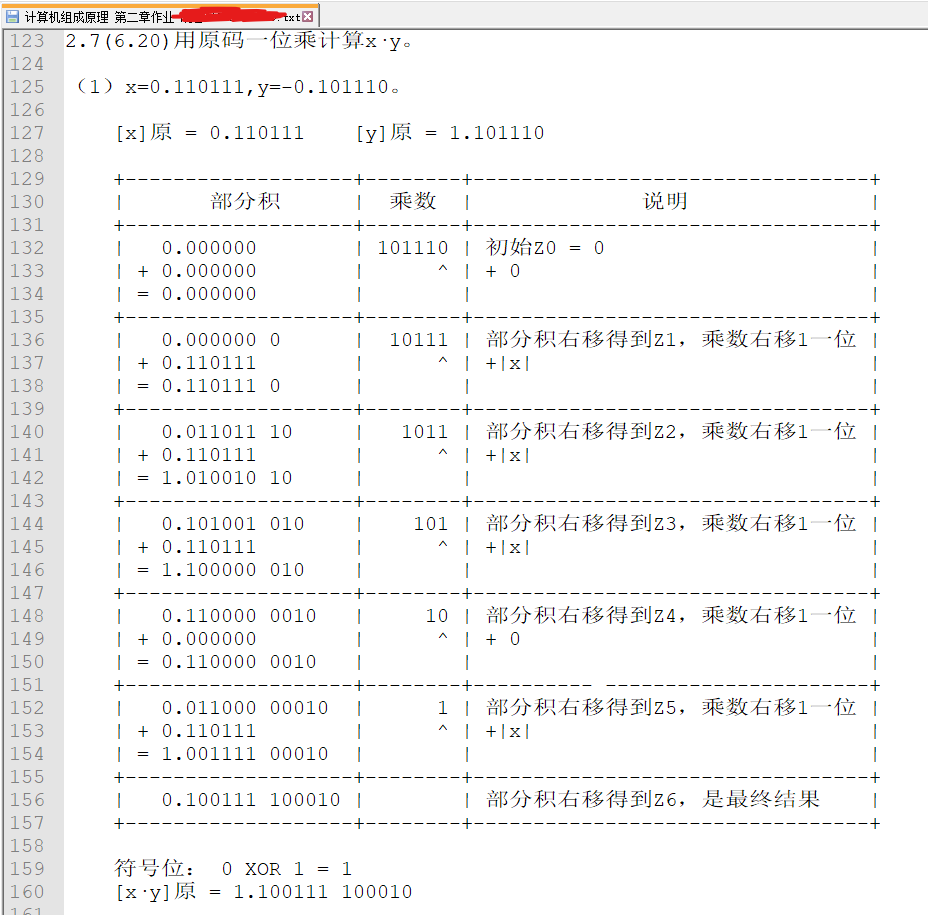
你要说让我用字符画个表格，那问题不大。可你要说让我在TXT里画个逻辑框图，我便要反问你了：你看我像逻辑框图不？我看你像逻辑框图。在TXT里面高端作图实在太复杂，遂决定使用Logisim搭建一个加法器，截图说明，实不成把Logisim的文件给老师一瞧，没准儿就行了。

我还记得上次用Logisim是在搭建8位计算机这篇文章里，今天一瞧它又更新了一个小版本号。遂找遍了各种移动硬盘和服务器，终于在谷歌云端硬盘里找到了备份的文件了，当时写文章的时候为了草草了事觉得简单，就没有公开文件，后来一想光看文章还并不是很明确，遂今天修改了文章加入了谷歌硬盘的下载链接。同样地，这篇文章写完之后也会开放下载32位加法器的Logisim文件。

题内话

引言

此处我不打算多介绍加法器的事情，还请感兴趣的各位移步本站的战略合作伙伴：谷歌搜索和维基百科。这里打算说一下传统的加法器有什么问题。

多位加法器的基本单元是一位全加器。最低位的全加器计算出「本位和」和「进位标志」，下一位全加器利用上一个加法器的进位标志来计算对应的「本位和」和「进位标志」，最终加法器的结构是一个链式结构，即后一位的计算依赖于前一位产生的进位标志。我们来计算一下耗时：假设一位全加器的延迟是$t_d$，那么计算n位加法的耗时就是$n t_d$，计算的位数越多，他就越慢，这样对于构造字长很长的计算机实属不利。

这样一来就引出了超前进位加法器，基于如下观察。

对于全加器的进位标志，计算公式是 $ C_i = A_iB_i + (A_i\oplus B_i)C_{i-1} $ ，如果把$A_iB_i$记作本地进位$d_i$，把$A_i\oplus B_i$记作传递条件$t_i$，那么公式就变成了$C_i = d_i+t_iC_{i-1}$，具体一点说，以第3位的进位标志为例，$C_3 = d_3 + t_3C_2 = d_3 + t_3(d_2 + t_2C_1)$，展开到这里，你会发现原本依赖于第2位的进位标志，变成了对第一位进位标志的依赖，如果继续展开，实际上任意一位进位标志的计算都将只依赖最初传入的进位$C_{-1}$。这样一来，知道加法的两个操作数和传入的进位，一下子就可以算出来所有位产生的进位标志，这样每一位的计算都将不再依赖上一位，而是可以在所有进位产生之后同时开始计算。

不过你可能也发现了，随着位数的增加，式子的项变得越来越多，这暗示着逻辑图和电路图也将变得十分复杂。通常的做法是将这样的并行加法定为较短的位数，然后再串成较长位数的加法器。这样分块的思想既没有复杂化电路，又比原来的设计快，所以何乐而不为呢。

搭建

这里我选定的是8位长度的传递链。其实就已经很长了，课上说的是4位的，一眼看过去电路就很复杂了，但是为了达到600ns完成计算，我也没想到好办法，只能增加到8位长度了。

按照上面的原理推出来每一位进位标志的公式，便可以实现电路了。粗略地看，8位的传递链长这样。

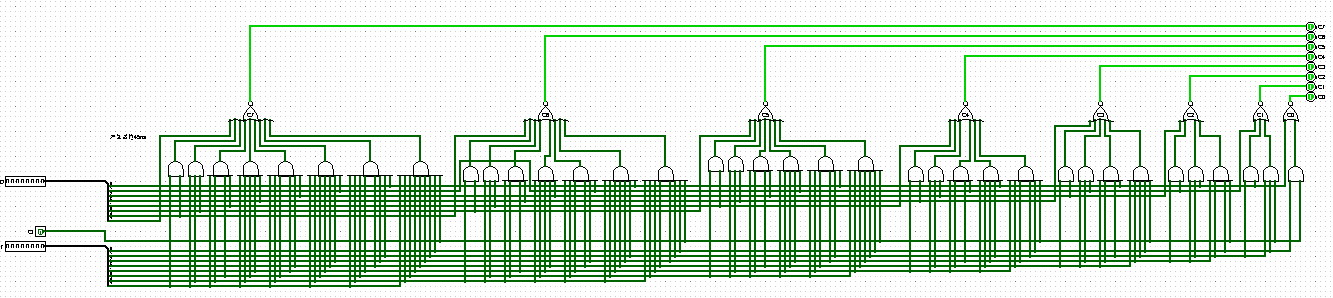
放大看看就是这样子的。

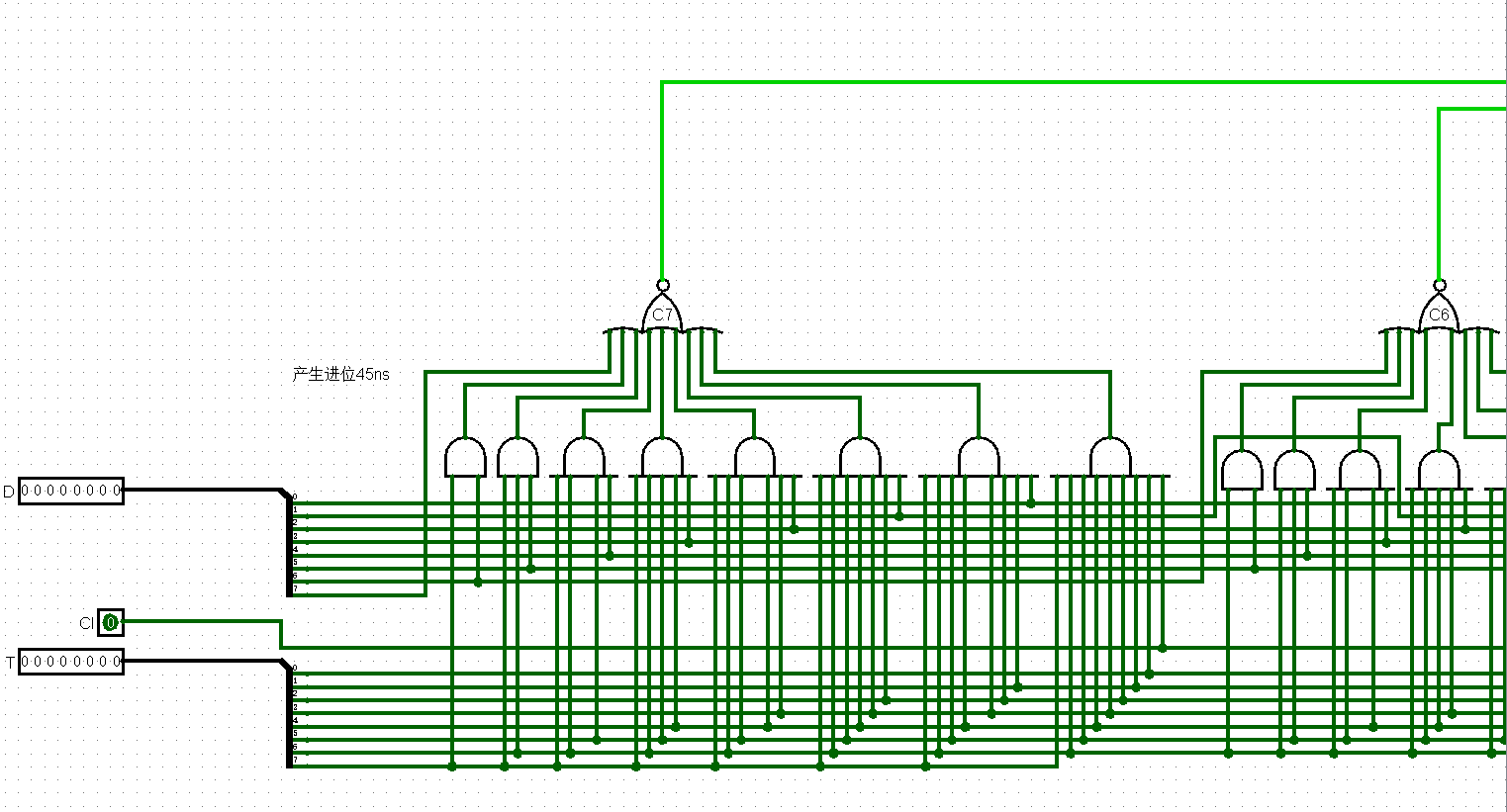
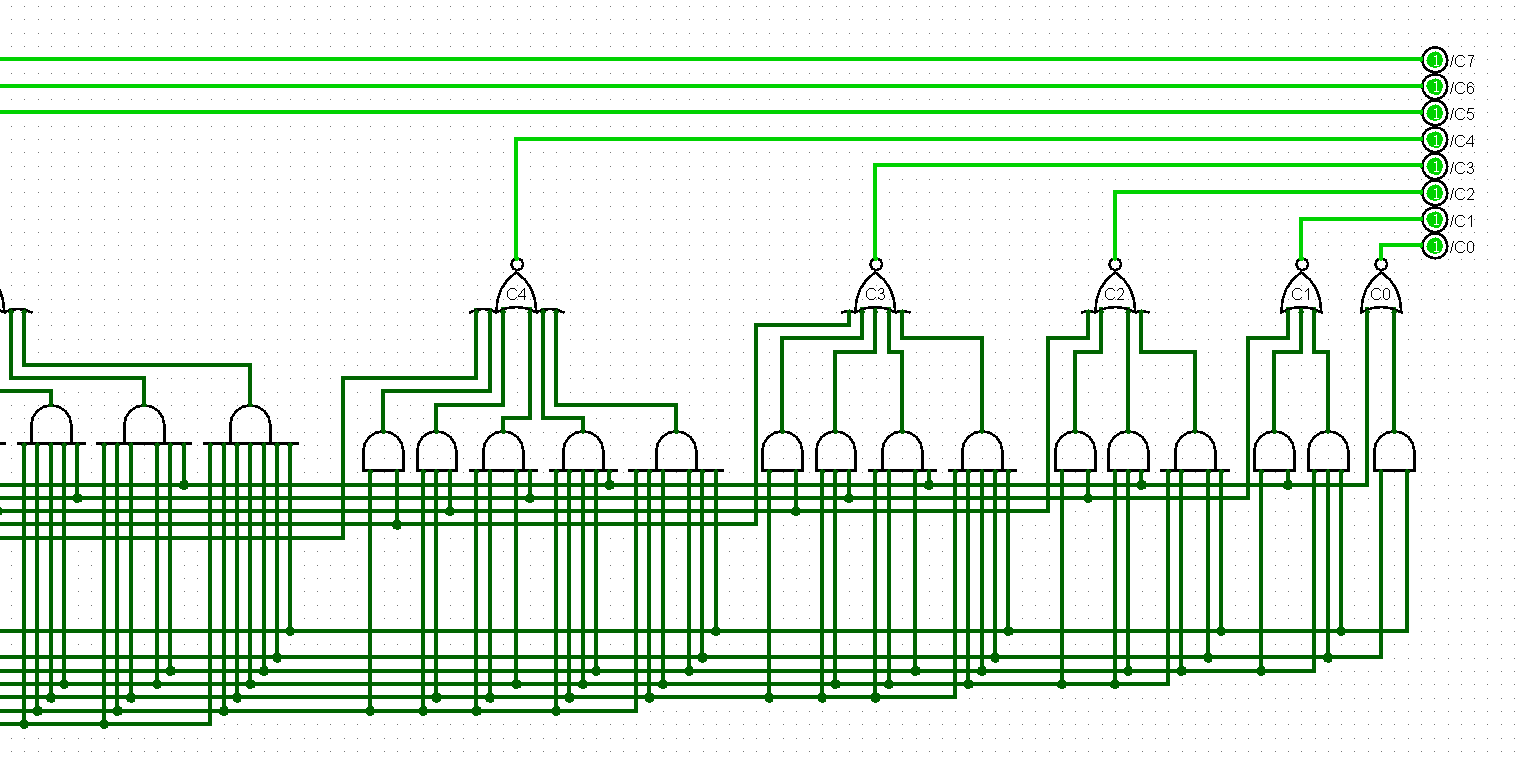
看起来蛮费劲的，这个没办法，只能硬着头皮来了。这时候就想到Verilog的好了，用代码把行为一描述，它自己就给你算出来逻辑关系了。不得不说在生产力上工具还是越高级越好。但是从乐趣的角度来看，还是这种中低端的有意思。

有了进位链，我们再整一个1位的全加器。由于题目要求说只能用与非门和与或非门（就是好几个与门接入一个或非门），所以我用NAND门实现了XOR，因为这里的全加器不需要再产生进位标志了，所以直接按照$S=A\oplus B \oplus C$来实现即可，如下示，还是挺简单的。

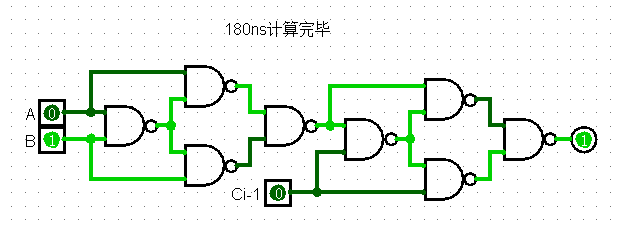
有了这两个组件，我们就可以搭建一个8位长的超前进位加法器了。这个加法器需要5个输入：每一位的本地进位和传递条件、两个操作数和$C_{-1}$，前面两个参数和最后一个参数用于生成每一位的进位标志，余下的参数则用来计算最终结果。这个模块长这个样子。

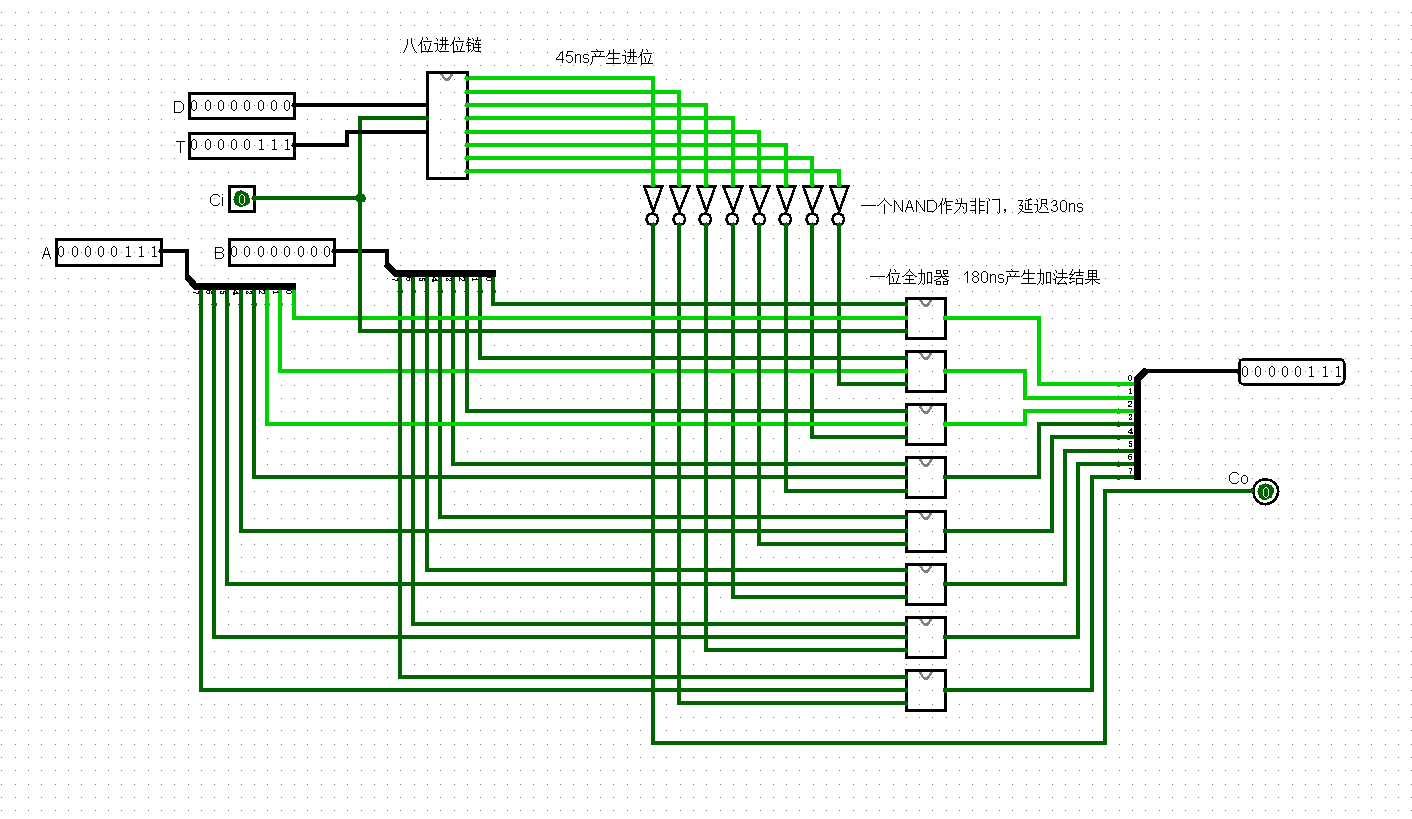
有了这些基础的单元，便可以很方便的构筑32位或者更多字长的加法器了。首先要计算出来本地进位和传递条件，还是因为题目限制，我用了NAND门实现了AND和XOR两个门，然后将八位超前进位加法器串起来，便是32位的加法器了。

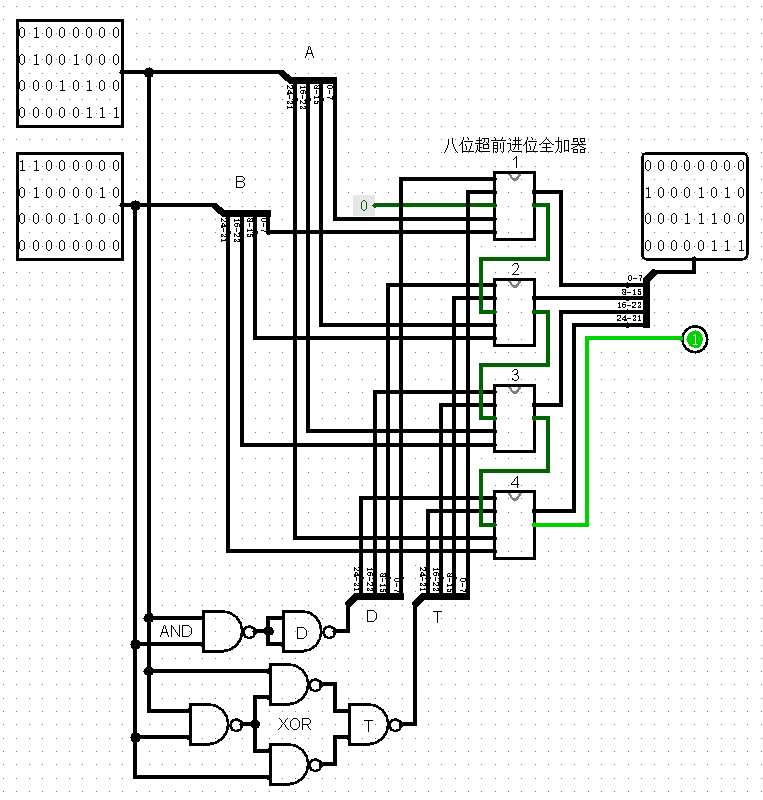
测试了一下问题不大，能够正确计算。OK了。

分析

东西是有了，可是合不合题目要求呢？这里我们来做一个时序约束。本来在Vivado里面，设定好时序约束之后程序会自动帮你计算，但是手动算一算，看一看工作过程也不失为一种乐趣。我们假设0时刻开始运算。

首先一件事情必然就是要计算出本地进位d和传递条件t，这两者的计算是并行的，d的计算用到了两层NAND，按照题目说的：

一个NAND延迟30ns，一个与或非门延迟45ns

d的计算延迟60ns，而t的计算用到了3层NAND，是90ns，所以90ns的时候才开始计算第一块，即进位标志C0到C7。传递链消耗45ns产生对应的进位标志，但由于是与或非门，传递链给出的进位标志是低有效，而我们需要高有效，所以由用了一层NAND作为非门来转换，小号30ns，一共花费75ns来产生C0到C7。产生之后计算结果Y0到Y7，和计算下一块进位标志C8到C15是同时进行的，因此75ns后C8到C15计算完毕。而计算结果则是用了两层XOR，一层XOR使用了3层NAND，那么也就是说计算结果耗时180ns。如此往复，在最后一块进位标志计算完成后，还要等待180ns将最后一块计算完成才算是结束。时间计算出来如下式：

90ns + 4 * 75ns + 180ns = 570ns

将计算过程转化为甘特图，更简单明了一些：

+--->本地进位
+----->传递条件
|     +---->进位C0~C7
|     |    +----------->结果Y0~Y7
|     |    +---->进位C8~C15
|     |    |    +----------->结果Y8~Y15
|     |    |    +---->进位C16~C23
|     |    |    |    +----------->结果Y16~Y23
|     |    |    |    +---->进位C24~C31
|     |    |    |    |    +----------->结果Y24~Y31
|     |    |    |    |    |           |
+---*-*----*----*----*-*--*--*---*----*--*---->t
^     ^    ^    ^    ^    ^           ^  ^
|     |    |    |    |    |           |  |
0     90  160  240  315  390         570 600

可见确实是达到了题目要求。挺好。

相关下载

32位加法器 - 超前进位

---

【歪门邪道】在 Logisim 中实现32位超前进位加法器 由 天空 Blond 采用 知识共享 署名 - 非商业性使用 - 相同方式共享 4.0 国际 许可协议进行许可。
本许可协议授权之外的使用权限可以从 https://skyblond.info/about.html 处获得。